


Project "Data Streaming" |
|||
| Members | |||
|
|||
| Support | |||
| Research supported by Deutsche Forschungsgemeinschaft, grant So 514/1-2. | |||
| Overview | |||
|
A data stream consists of a long sequence of data items, whose length restricts the amount of resources that is available to process the data and the kind of access to the data. In general, the amount of data is too large to store it in main memory. Often it is even larger than the capacity of modern hard disks. As a result, the data has to be processed on the fly, and the only possible access to the data is sequential reading. Typical examples of data streams are network traffic data, measurements of sensor networks or webcrawls. The task of a streaming algorithm is to read the data in one or a few passes and to maintain, at any point of time, a sketch of the already seen data. Usually, a streaming algorithm is only allowed to use local memory that is polylogarithmic in the size of the input stream, and it is only allowed to perform one or a polylogarithmic number of passes. The aim of the project is to develop algorithms in geometric streaming models and to analyze the relations between geometric streaming models. We subdivide our project into the following areas:
ClusteringClustering is a process to partition a given set of objects into subsets called clusters, such that objects in the same cluster are similar and objects in different clusters are dissimilar. Such a process can be applyed to simplify a large amount of data by replacing each cluster by one or a few representatives. In this way, clustering methods are very useful to analyze data streams. Metric EmbeddingsMetric embeddings are another important tool in the analysis of data streams. Here, we are especially interested in methods that embed a set of high-dimensional points into a low-dimensional space, such that a large fraction of all the pairwise distances between the points is almost preserved and only a small fraction of all the distances can be arbitrarily distorted. Since such an embedding can be stored in small space and much information about a set of points can be obtained from the corresponding pairwise distances, applying this technique results in a compact representation of the points in the input stream. Analysis of Huge GraphsThere are two models which are typically used to analyze huge graphs: the adjacency model and the incidence model. In the first model, the input graph is given as a stream of edges, which occur in an arbitrary order. In the second model, all edges incident to the same node occur as a continuous subsequence one after the other in the input stream. In this scenario, our focus is to count the number of occurences of a user-defined subgraph in a huge graph given as a stream of edges. We have already developed some algorithms that approximate the number of triangles. In the future, we would like to automate these methods, such that it is also possible to count the occurences of subgraphs that consist of a bigger number of nodes. Decision Tree LearningDecision tree learning is used for automatic classification of objects. The task is to assign objects to a finite set of classes. During the learning phase, the classification system gets some training data consisting of several object-class pairs as input. Based on these object-class pairs the system constructs a decision tree. After the learning phase, the constructed decision tree is used to automatically classify objects with unknown class. In many cases, the considered objects can be represented as points in an Euclidean space. We are especially interested in those scenarios, where the training data consists of a set of point-class pairs. Our goal is to develop streaming algorithms for decision tree learning with provable quality. Relations between Geometric Streaming ModelsDuring the last decades, theoretical computer scientists invented many different streaming models. In geometry, there is the insertion-only model, the dynamic model, the reset model, and the sliding window model. In the insertion-only model, the input is a sequence of insert operations of points. The dynamic model permits delete operations in addition to insert operations. In the reset model, the input is a sequence of update operations, where each update is of the form "the new position of the point with index i is p". In the sliding window model, we get a possibly infinite sequence of points as input, but, at any point of time, the computations should only take the n most recent points into consideration. It is easy to see that every algorithm that works in the dynamic model is also suitable for the insertion-only model. Are there any other provable relations between the different streaming models? In the following, we present three selected works which evolved from the project "Data Streaming". |
|||
| Selected Topics | |||
StreamKM++: A Fast Streaming Implementation for k-Means ClusteringIn the k-means clustering problem, one is given an integer k and a set of points in ℜd. The goal is to compute a set of k centers, such that the sum of the squared distances between each point and its nearest center is minimized. 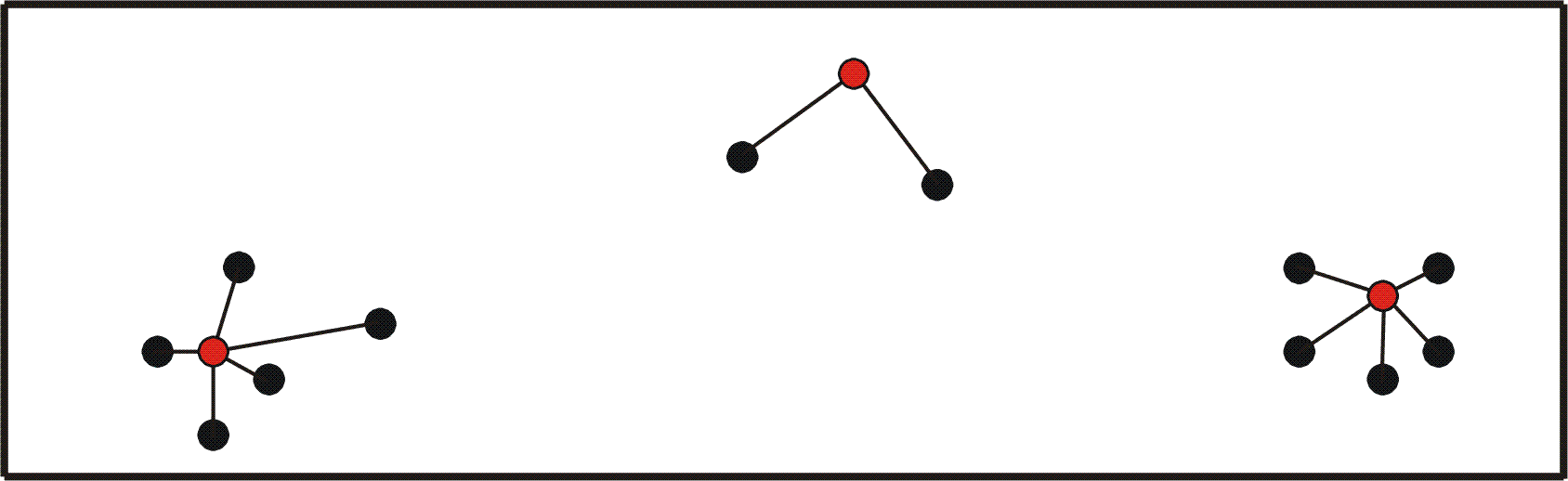
Illustration of k-means clustering for a point set in the plane and for k = 3. The red points are the centers. In cooperation with the project "Entwicklung einer praxisnahen Theorie für Clusteringalgorithmen durch datengetriebene Modellierung und Analyse" (DFG Schwerpunktprogramm 1307), we developed and implemented a new k-means clustering algorithm that efficiently processes large data sets. We call our method StreamKM++. StreamKM++ takes a random sample of the data stream based on the seeding strategy of k-Means++ and weights each sample point. The chosen weight of a sample point corresponds roughly to the number of input points in its Voronoi cell. Then StreamKM++ computes a clustering on the weighted sample set. We compared our algorithm experimentally with the two streaming implementations BIRCH and StreamLS, which are both well-known and frequently used for processing data streams. Our experiments show that StreamKM++ is slower than BIRCH, but in terms of quality it is significantly better than BIRCH. Furthermore, one can see that StreamKM++ and StreamLS are comparable in terms of quality, but our method scales better with the number of clusters. While for about 10 centers or less StreamLS is sometimes faster than our algorithm, for a larger number of center our algorithm easily outperforms StreamLS. Since synthetical datasets like Gaussian distributed points near some uniformly distributed centers in ℜd tend to be too good-natured, we used only real-world datasets to get practical relevant results. Our main source for data was the UCI Machine Learning Repository. For our experiments, we have chosen datasets that are too large to be stored in main memory, so that we had to perform a sequential reading from hard disk. One of the used datasets consists of 2 458 285 entries of commercial data, where each entry has got 68 dimensions. Our experimental results for this dataset are illustrated in the following diagrams. 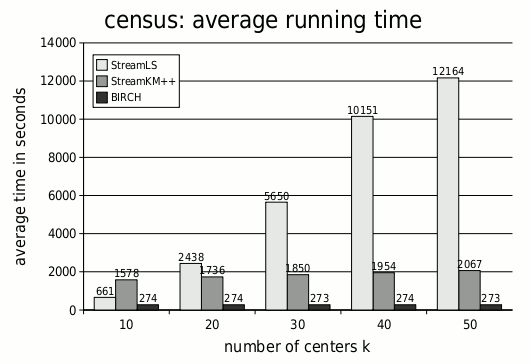
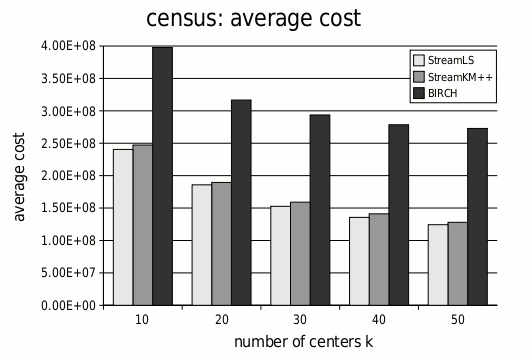
Experimental results for the dataset Census 1990 (available at the UCI Machine Lerning Repository). Each computation was performed on a DELL Optiplex 620 machine with 3 GHz Pentium D CPU and 2GB main memory, using Linux 2.6.9 kernel. All algorithms were compiled using g++ from the GNU Compiler Collection on optimization level 2. Since StreamLS and StreamKM++ are methods whose quality and running time dependent on random experiments, we repeated each experiment several times and output the mean values of the running time and cost. We also gave a theoretical justification of our approach. For low dimensions, we were able to prove that if we take a sample set by using the k-Means++ strategy and weight each sample point by the number of input point in its Voronoi cell, then the resulting weighted point set is a corset for the k-means clustering problem. In general, a coreset is a small weighted point set, which approximates an unweighted input point set in terms of a given problem. |
|||
Facility Location in Dynamic Geometric Data StreamsIn the model of dynamic data streams, the input is a sequence of insert and delete operations of points from a low-dimensional, discrete space {1,...,Δ}d. We investigated a variant of the facility location problem. In this variant, one is given a set of clients that have to be served by a set of facilities. It is possible to open a facility at any client for a given cost of f. The cost of serving a client is proportional to its distance to the nearest facility. We call the total cost that arise for opening the facilities opening cost and the total cost that arise for serving all clients connection cost. The goal is now to minimize the sum of opening and connection cost. Since the number of open facilities can be as large as the considered point set and the available memory space is only polylogarithmic in the cardinality of the point set, we cannot compute a solution in the streaming model. Instead, we focus on approximating the cost of a solution. We developed a randomized algorithm that maintains a constant factor approximation for the cost of the facility location problem over dynamic data streams. For the computations, our algorithm uses a polylogarithmic number of nested squared grids over the point space. The side length of a cell in the coarsest grid is Δ and each cell of any grid containes 2d equal sized cells of the next finer grid. The idea is now to define a certain partition of the input space based on the grids and to relate this partition to the cost of the facility location problem. To do so, we proceed in a similar way like building a quadtree. We start with the partition that consists of all cells in the coarsest grid. Then, we recursively split each cell, which contains a heavy, smaller cell (a heavy cell that belongs to a finer grid) or whose direct neighborhood contains a heavy, smaller cell, into 2d equal sized cells (cells of the next finer grid). We call a cell heavy if the product of the side length of the cell and number of points inside the cell is at least f. After obtaining the final partition, the opening cost can be estimated by counting the number of heavy cells in the partition. The connection cost is approximated by summing up over all cells the number of points inside the cell times the side length of the cell. Both counting problems can be reduced to problems that estimate the number of distinct elements in a data stream and for which already efficient algorithms exist. The working method of our algorithm is illustrated by the following figure. 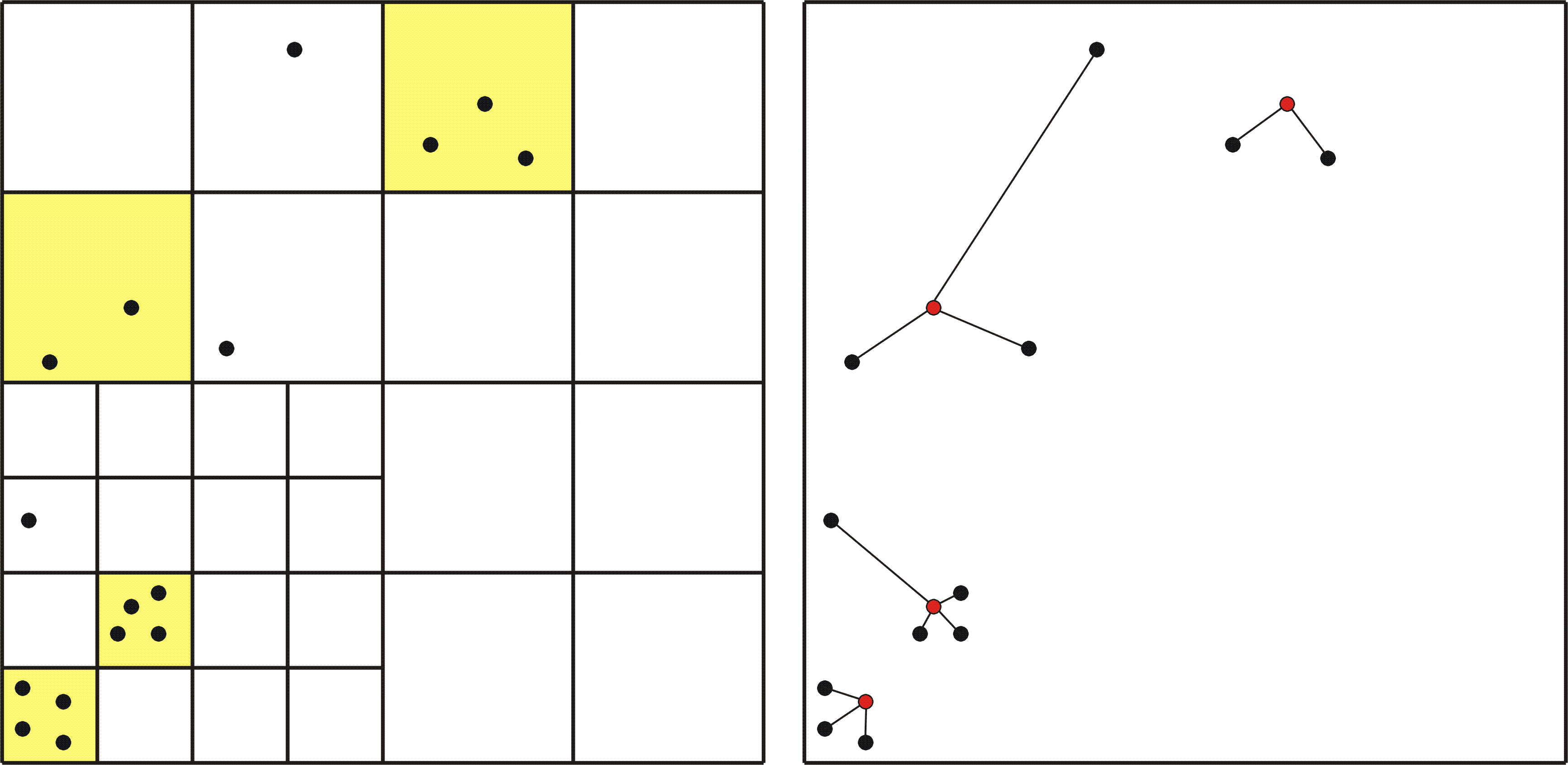
The left figure shows the partition of a point set in the plane for Δ = 8 and f = 4. The heavy cells of the partition are marked by the yellow background. The right figure shows the solution whose cost is approximated by the streaming algorithm. The red points are the facilities and the line segments indicate the connections between the clients and the facilities. |
|||
| Awards | |||
|
In 2009 the group's member Christiane Lammersen won the Google Anita Borg Memorial Scholarship 2009. Google established the Anita Borg Memorial Scholarship in 2003 to encourage undergraduate and graduate women to complete degrees in computer science and related fields, to excel in computing and technology, and to become active role models and leaders in the field. Scholarships are awarded based on the strength of the candidates, academic performance, leadership experience and demonstrated passion for computer science. |
|||
| List of Publications | |||
|